
21 Mar Are Cereal Companies Bad at Math?
This post is a redesign of Kris’s Cereal Box digital fabrication project. Although the tweaks that I describe move Kris’s elementary lesson into the middle school and high school realm, it could be altered to be more of a discovery-type experience for elementary students familiar with digital fabrication and ModelMaker.
I came across a lesson this weekend that very simply stated that companies like General Mills and Post must have some reason for creating cereal boxes in their current dimensions other than “bottom line” economic decisions. The rationale was simple: If companies that make cereal really wanted to maximize their profits, then they would reconsider the way in which cereal was packaged. Cereal companies could sell the same amount of bran flakes and crunchy goodness (volume) by redesigning the packaging (surface area) so that it resembled a cube. Less surface area (packaging materials) and equal volume = lower manufacturing costs. Plus, there would be ecological benefits.
This afternoon I pulled out something that I have not touched for a truly mathematical purpose since high school: a ruler. I wanted to test this lesson’s underlying ideas. I grabbed my box of Total Cinnamon Crunch off the refrigerator, and calculated the following dimensions using my ruler:
Length: 7 5/8 inches
Width: 2 inches
Height: 10 1/8 inches
I had to do some fraction-decimal conversions in order to re-create the 3D model below in FabLab ModelMaker, a CAD software program designed for elementary and middle school students. That was worthwhile as a standalone activity if readers are thinking about mathematical procedures, processes, and algorithms.
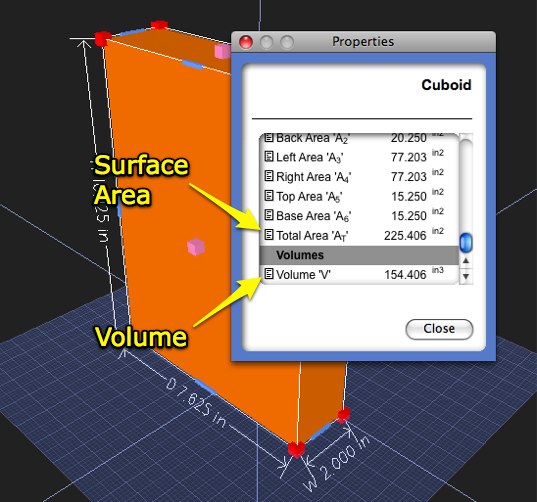
The following image is a 3D representation of my cereal box (without graphics).
I have to admit that I did not spend the time calculating the cereal box’s surface area and volume. I actually used ModelMaker’s properties to give me the answer for surface area and volume.
SA: 225.406 inches²
Volume: 154.406 inches³
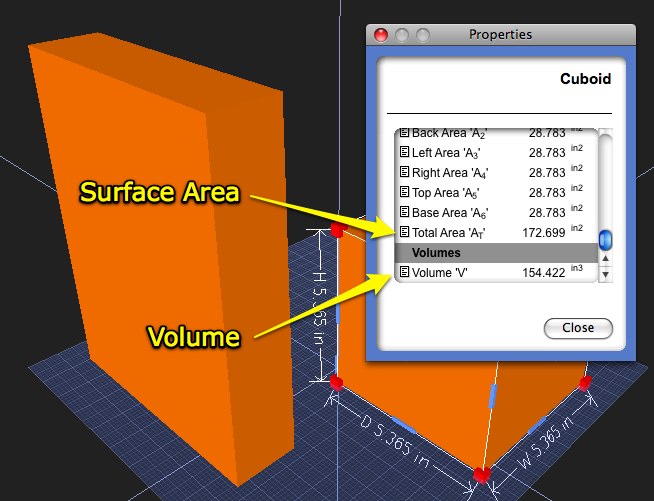
To test the hypothesis, I took the cubic root (I forget the mathematical terms) of the volume, 154.406 inches cubed. The rounded answer was a length, width, and height of 5.365 inches (rounded), the dimensions for my cube. The result? A package that has relatively similar volume (disregarding variations due to rounding) and a much smaller surface area!
If I was going to engineer a cereal box, I would not begin with off-the-shelf examples as a starting point. Greater surface area for a given volume equals higher manufacturing costs and greater waste, a practice that has to have some origin… Why do companies like General Mills and Post continue to produce cereal boxes that are clearly economically and ecologically inferior? The answer to this question is likely an entirely new learning strand that relates to social studies…
Is there truth to the idea that packaging relies more on the Golden Mean then the economic bottom line?
Note
There is a great post on Scientific American about “Juice Box Geometry” that relates to this post. I encourage readers of this post to check it out!
Image Reference
Joyce, M. (2008, August 17). Fruit Loops. Retrieved 18 May 2015, from https://www.flickr.com/photos/hckyso/2771942938



Edmonton Casper
Posted at 17:51h, 04 NovemberThe reason that cereal boxes aren’t cubes is so that they attract buyers with their branding, which needs a large area to catch the eye, and the cardboard is so thin, the surface area problem doesn’t matter too much.